（二）連續性校正公式　χ2檢驗是以連續的光滑曲線做根據的，當自由度為1時，χ2檢驗所得的概率容易偏低，因些需要校正，校正后的χ2值比不校正的小一些，校正公式是：

　　 （3.7）　

　　公式中A-T前后兩條直線是絕對值的符號。

　　將表3.5資料代入式（3.7）得：

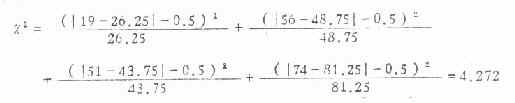
　　檢驗兩個率相差的顯著性時（此時自由度為1），理論上都可用校正公式。但當用公式（3.5）求出的χ2值小于3.84時，相應的P值大于0.05，表示兩個率相差不顯著，校正后χ2值更小，仍得同樣結構，就無須校正；當用未校正公式求出的χ2值遠遠超過3.84時，校正后的結論仍相同，在此種情況下也可不校正；當自由度為2及以上時，則不必校正。

　　當用公式（3.5）求出的χ2值略大于3.84時，校正最為必要，往往會改變原來的結論，舉例如下。

　　例3.2表3.7是六六六粉的兩種配方進行野外煙劑滅黃鼠實驗的觀察結果。

表3.7　六六六粉兩種配方滅黃鼠的效果

	煙薰后鼠洞情況		合 計 　　(實驗觀察洞數)	滅洞率 　　（%）
	未盜開	盜　開
04號配方	13(16.63)	9(5.37)	22	59.1
05號配方	80(76.37)	21(24.63)	101	79.2
總 計	93	30	123	75.6

　　現用公式（3.5）及式（3.6）分別計算χ2值如下：

　　校正后的χ2值小于3.84，P>0.05，在α=0.05的水準處接受H0，認為兩種配方滅黃鼠效果無顯著差異，這相結論是比較合理的，如果不經校正就會得出錯誤的結論。

　　（三）四格表中求χ2的專用公式　用上述基本公式（3.5）求χ2值，需要求出與實際頻數一一對應的理論頻數，運算較繁。在四格表中，用下列專用公式較為簡便。

　（3.8）

　　式中a、b、c、d為四格表中的實際頻數，N表示總例數（即N=a+b+c+d）。

　　現仍以表3.5資料為例，先寫成四格表形式，如表3.8。

表3.8　四格表求χ2值專用公式的符號

	死 亡	生存	合 計
抗凝血組	19(a)	56(b)	75(a+b)
對照組	51(c)	74(d)	125(c+d)
	70（a+c）	130(b+d)	200(N)

　　將實際頻數代入式（3.8）得，

　　這里用專用公式求得的χ2值與前面用基本公式求得的結果完全不同，有時這兩個公式求得的結果小數點后幾位可能稍有出入，這是由于受小數四舍五入的影響。

　　前面已介紹了連續性校正公式（3.7），為使運算更為簡便，下面列出專用公式的連續性校正公式（3.9），并以表3.8資料代入計算如下：

（3.9）

　　所得結果與式(3.7)求得的一致。

　　二、多個率或多個構成比的比較

　　（一）2×K表的專用公式，前面已討論了，兩個率的比較用四格表專用公式計算χ2值較為簡便。如果是多個率比較，就要列成2×K表。這里的K暫為所比較的組數，2為每個組內所劃分的類型數。求χ2值時本可用基本公式計算，但以用下列專用公式為便：

　　　　　　　　　　　　 （3.10） （3.11）

　　　　　　　　表3.9　2×K表形式之一

a1 　　a2 　　┆ 　　┆	b1 　　b2 　　┆ 　　┆	n1 　　n2 　　┆ 　　┆
∑ai	∑bi	N

　　公式中符號的意義參閱表3.9，以上兩個公式的計算結果是完全一樣的。

　　例3.3 某地觀察磺胺三甲氧吡嗪加增效劑（吡嗪磺合劑）預防瘧疾復發的效果，用已知有抗瘧疾復發效果的乙胺嘧啶和不投藥組作對照，比較三組的瘧疾復發率，資料如表3.10，問三組復發率有無顯著差別？

表3.10　三個組的瘧疾復發率

組　別	觀察例數	復發例數	復發率（%）
吡嗪磺合劑 　　乙胺嘧啶 　　對　照	1996 　　473 　　484	76 　　27 　　53	3.81 　　5.71 　　10.95
合　計	2953	156	5.28

　　χ2檢驗步驟如下：

　　1．將表3.10資料寫成2×K表形式，見表3.11。注意：這里必須把各組的觀察例數分為復發和未復發兩部分，這樣表3.10就為寫成2×3表。

表3.11　三個組瘧疾復發率的比較

	復發	未復發	合 計
吡嗪磺合劑	76	1920	1996
乙胺嘧啶	27	446	473
對 照	53	431	484
合 計	156	2797	2953

　　2．H0：三個總體復發率相同

　　H１：三個總體復發率不全相同

　　α=0.05

　　3．求χ2值 將表3.11的數值代入式（3.10）（因為在表3.11中，各組的a值較小，計算較方便）得：

　　4．求自由度，確定P值，作結論

　　ν=（K-1）（2-1）=（3-1）（2-1）=2，查χ2值表得χ20.01(2)=9.21，本例χ2=39.92>χ20.01(2)，P<0.01,在α=0.05的水準處拒絕H0，接受H1，即三個組的復發率有顯著差別。

　　本例的結論是三個組的復發率有顯著差別，因此，還需進一步說明三組中那兩組有差別，可用四格表對每兩個率進行假設檢驗。本例的檢驗結果是：吡嗪磺合劑與對照組比（P<0.01），乙胺嘧啶組與對照組比（P<0.01），而吡嗪磺合劑與乙胺嘧啶比（P>0.05），說明吡嗪磺合劑有預防瘧疾復發的作用，其效果不低于乙胺嘧啶。

　　本例2×K表的2是指得發、未復發兩項，K為比較的組數，K=3。如果比較組數只有2，而構成每組的項數則多于2，如甲狀腺腫的型別構成可分為彌漫型、結節型、混合型三種。這類資料亦同樣可用2×K表專用公式進行檢驗。這時把2作為比較組數，K作為項數，檢驗方法同上，表3.12是2×K表的另一種形式。

表3.12　2×K表形式之二

a1	a2	……	∑ai 　　∑bi
b1	b2	……
n1	n2	……	N

　　例3.4，為研究不同地域甲狀腺型別的構成有無顯著差別，某省對兩個縣的居民進行甲狀腺腫調查，得資料如表3.13，問甲乙兩縣各型甲狀腺腫患者構成比有無顯著判別？

上一頁  [1] [2] [3] 下一頁