X2（稱卡方）檢驗用途較廣，但主要用于檢驗兩個或兩個以上樣本率或構成比之間差別的顯著性，也可檢驗兩類事物之間是否存在一定的關系。

　　一、兩個率的比較

　　（一）X2檢驗的基本公式　下頁末行的例3.1是兩組心肌梗塞病人病死率的比較，見表3.5，其中對照組未用抗凝藥。兩組病人的病死率不同，抗凝藥組為25.33%，對照組為40.8%。造成這種不同的原因可能有兩種：一種是僅由抽樣誤差所致；另一種是兩個總體病死率確實有所不同。為了區別這兩種情況，應當進行X2檢驗。其基本步驟如下：

　　1．首先將資料寫成四格表形式，如表3.6。

　　將每個組的治療人數分為死亡與生存兩部分，各占四格表中的一格，這些數字稱為實際頻數，符號為A，即實際觀察得來的數字。

　　2.建立檢驗假設　為了進行檢驗，首先作檢驗假設：兩種療法的兩總體病死率相等，為35%（即70/200），記為H0：π1=π2。即不論用或不用抗凝藥，病死率都是35%，所以亦可以換一種說法：病死率與療法無關。

　　上述假設經過下面步驟的檢驗后，可以被接受也可以被拒絕。當H0被拒絕時，就意味著接受其對立假設即備擇假設H1。此例備擇假設為兩總體病死率不相等，記為H1：π1≠π2

　　因為我們觀察的是隨機現象，所以無論是接受或拒絕H0都冒有一定風險，即存在著錯判的可能性。一般要求，當錯誤地被拒絕的概率α不超過一定的數值，如5%（或0.05），此值稱為檢驗水準，記為α=0.05。

　　3．計算理論頻數　根據“檢驗假設”推算出來的頻數稱理論頻數，符號為T。計算方法如下：假設兩總體病死率相同，都是35.0%，那么抗凝血組治療75人，其死亡的理論頻數應為75×35.0%=26.25人，而生存的理論頻數為75-26.25=48.75人。用同樣方法可求出對照組的死亡與生存的理論頻數，前者為43.75人。后者為81.25人。 然后，把這些理論頻數填入相應的實際頻數格內，見表3.6括號內數字。

　　計算理論頻數也可用下式（3.4）

　　TRC=nRnC/N (3.4)

　　式中，TRC為R行與C列相交格子的理論頻數，nR為與計算的理論頻數同行的合計數，nC為與該理論頻數同列的合計數，N為總例數。

　　例如；表3.6第一行與第一列相交格子的理論頻數（T1１）為

　　T1１＝ 75×70/200=26.25

　　用兩種方法計算，結果是相同的。

　　4．計算χ2值，計算χ2值的基本公式為：

　　X2=∑（A-T）2/t 　（3.5）

　　式中，A為實際頻數，T為理論頻數，∑為求和符號。

　　將表3.6里的實際頻數與理論頻數代入式（3.5）即求得χ2值。此例χ2=4.929。

　　從式3.5中可看出，實際頻數與理論頻數之差（A-T）愈小，所得的χ2值就愈小，理論頻數是根據檢驗假設推算出來的，若與實際頻數相差不大，說明假設與實際情況符合，于是就接受H0，認為兩病死率無顯著差別；反之，若（A-T）大，則χ2值亦大，說明假設與實際不符，就拒絕假設，認為兩病死率有差別。但χ2值大還是小，要有一個比較的標準，要查χ2值表（附表1），查χ2值表前先要定自由度。

　　5．求自由度　自由度是數學上的一個名詞。在統計中，幾個數據不受任何條件（如統計量，即樣本特征數）的限制，幾個數據就可以任意指定，稱為有幾個自由度。若受到P個條件限制，就只有n-p個自由度了。例如在四格表中有四個實際頻數，如沒有任何條件限制，則4個數字都可任意取值，有4個自由度，當a+b,，c+d，a+c，b+d都固定后，在a、b、c、d四個實際頻數中，只能有一個頻數可任意指定了，因此，四格表的自由度為1。其計算公式為：

　　ν=（R-1）（C-1） （3.6）

　　式中，ν為自由度，R為橫行數，C為縱列數。

　　四格表有2行和2列（注意：總計與合計欄不算在內）。因此ν=(2-1)(2-1)=1。

　　6．求P值，作結論　根據自由度查χ2值表（附表1）。此表的左側ν為自由度，表內數字χ2值，表的上端P是從同一總體中抽得此樣本χ2值的概率。三者關系是：在同一自由度下，χ2值越大，從同一總體中抽得此樣本的概率P值越小；在同一P值下，自由度越大，χ2值也越大。χ2值與概率P呈相反的關系。χ2檢驗的常用界值為：

　　χ2<χ20.05（）P>0.05 在α=0.05水準處接受H0，差別不顯著

　　χ20.05≤χ2<χ20.01()0.05≥P>0.01 在α=0.05水準處拒絕HO，接受H1，差別顯著

　　χ2≥χ20.01（）P≤0.01 在α=0.01水準處拒絕HO，接受H1，差別顯著

　　這里α是預定的檢驗水準。χ20.05（）是當自由度為ν時與P=0.05相對應的χ2 值，簡稱5%點，χ20.01（）是與P=0.01相對應的χ2 值，簡稱1%點。

　　當ν=1時，χ20.05（1）3.84，χ20.01（1）=6.63。本例自由度為1，求得χ2=4.929,介于3.84與6.63之間，或寫成χ20.05（1）<χ2<χ20.01（1）。由于與3.84對應的縱行P=0.05，與6.63對應的縱行P=0.01，因此與樣本χ2=4.929相應的概率介于0.05與0.01之間，寫成0.05>P>0.01。在α=0.05水準處拒絕H0，接受H1，兩總體率不等。對照組的病死率較抗凝血組高。

　　在α=0.05水準處拒絕H0，說明若在同樣情況下作100次判斷，將有5次或不到5次的機會，將原沒有差別的兩總體率錯判為有差別，或說這樣判斷犯I型錯誤的概率不超過5%。

　　下面將實例的檢驗步驟集中列出。

　　例3.1　兩組心肌梗塞病人的病死率可見于表3.5，其中對照組未用抗凝藥。抗凝血組病死率為25.33%，對照組為40.80%，問兩組病死率有無顯著差別？

表3.5　兩組心肌梗塞病人病死率比較

組別	治療人數	死亡人數	病死率（%）
抗凝血組	75	19	25.33
對 照 組	125	51	40.80
總 計	200	70	35.00

　　檢驗步驟如下：

　　1．將資料列成四格表形式，如表3.6。

表3.6　四格表式樣

	死亡	生存	合計
抗凝血組	19(26.25)	56(48.75)	75
對照組	51（43.75）	74(81.25)	125
總 計	70	130	200

　　2．H0：兩療法的總體病死率相同，即π1=π2

　　H1：兩療法的總體病死率不同，即π1≠π2

　　α=0.05

　　3．求理論頻數

　　抗凝血組：

　　死亡人數為75×35.0%=26.25人

　　存活人數為 75-26.25=48.75人

　　對照組：

　　死亡人數為125×35.0%=43.75人

　　存活人數為 125-43.75=81.25人

　　把理論頻數填入相對應的實際頻數格內，見表3.6括號內數字。

　　4．求χ2值 將表3.6里的數值代入式（3.5）得，

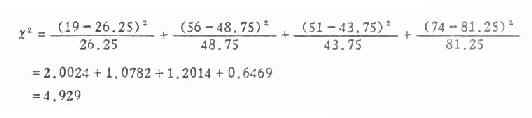
　　5．求自由度，確定P值，作結論

　　ν=（2-1）（2-1）=1，χ2 0.05（1）=3.84,χ2 0.01（1）=6.63,

　　本例χ2 =4.929,χ2 0.05（1）<χ2 <χ2 0.01（1），則0.05>P>0.01，在α=0.05水準處拒絕H0，接受H1，即兩總體病死率不等，對照組病死率較抗凝血組高。

　　上例告訴我們，兩個樣本病死率一大一小，在未作檢驗之前，很難說它們兩總體率是否有差別，為了作出正確判斷，作X2檢驗。先假設兩總體病死率相同，推算理論頻數，由實際頻數與理論頻數計算χ2值，二者相差越大，χ2值也越大。本例得χ2=4.929，根據自由度為1時的χ2分布推斷，從同一總體內抽樣，出現χ2值等于或大于4.929的概率較小，每一百次中在5次以下，1次以上，因此檢驗假設被拒絕，而判斷為有顯著差別。

[1] [2] [3] 下一頁